输出电路能产生的电压变化的最大速率。它被测量为相对于时间的电压，数据表中使用的典型单位是V/µs。因此，它表明了其输出电压（Vo）变化的速度。

  在处理交流信号或作为比较器时，您必须要格外注意此参数。转换速率越大，对应的运算放大器带宽就越高。

  ① 运算放大器的输出不能对输入的变化做出即时响应。因此，从输入变化到输出变化，我们有一个不可避免的延迟。

  ② 当运算放大器以负反馈配置连接时，在某些情况下，这种延迟将导致施加到反相输入端子的电压和施加到非反相输入端子上的电压之间的大差。这种大的差分电压以输出电压线性增加（或减少）的方式改变了差分对输入级的行为，即VOUT（t）=SR×t。转换速率（SR）受到补偿电容量的强烈影响。

  转换速率公式为SR=ΔVout/Δt。转换速率单位为V/μs或伏特每秒。见图1。

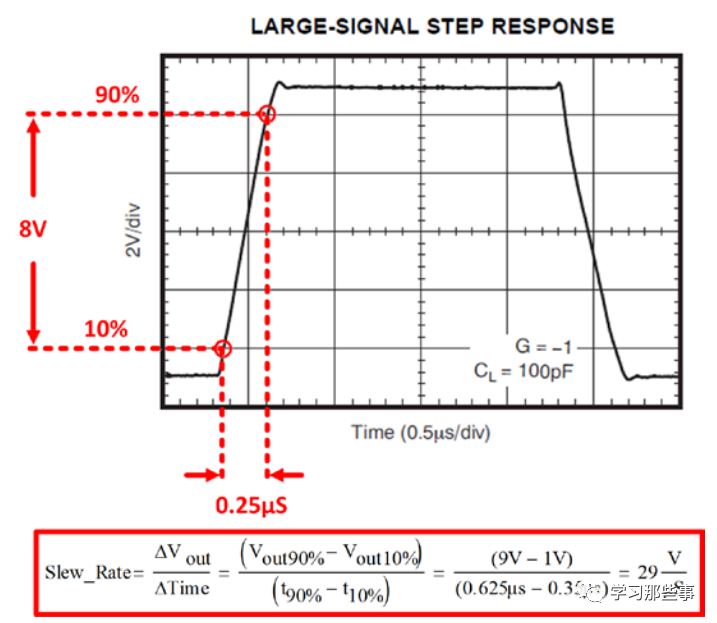
  SR是输出电压幅度相对于时间从10%到90%的最大变化。SR属于大信号现象，运放的限流和本征级饱和在很大程度上导致了SR的产生。

  两个重要的概念与运算放大器的速度有关，如转换速率和带宽。两者共同决定阶跃响应的总时间。

  回转速率可以限制通过运算放大器的任何信号变化。回转是一种非线性效应。如果正弦输入信号乘以运算放大器的增益导致斜率高于运算放大器的转换速率，则输出波形的一部分将是正弦曲线的直线而不是弯曲部分。

  因此，回转能改变信号的形状，因此是失真的来源，而不单单是振幅或相位的改变。因此，回转可能会改变或扭曲信号形状。

  带宽是对信号中的微小变化做出一定的反应的最高速率。在直流偏压下，运算放大器能够最终靠使用静态功率来设计，以便它接受小信号或相当小的振幅信号。当这些信号通过傅立叶变换分解时，它会给你添加从小频率到大频率的极其不同的频率。

  当带宽更高时，运算放大器能够增加更高频率的信号，因此它们具有高速度。信号增益为1/√2（0.707）的频率，则它是运算放大器的完美带宽值。因此，这是运算放大器能够最终靠预期行为发挥作用的最高频率。

  当我们处理正弦信号时，运算放大器在高频下会失去增益，而当我们处理瞬态事件时，相同的基本机制限制了输出信号的最大变化率。然而，重要的是要认识到频率响应和转换速率是不同的现象，并且这两种现象的影响是根本不同的。

  回转速率是放大器对输出中的变化做出一定的反应的速率。在不同频率、相同振幅的不同波形中，我们大家可以注意到每个正弦波的振幅都是相同的；具有最大频率的信号在每单位时间内具有最大电压变化。

  因此，当频率增加时，转换速率具有逐渐的效果，直到在转换速率不能与波形的频率继续的地方达到阈值。

  因此，在那之后，高频响应可能会受到转换速率的影响，导致信号在固定点上严重失线

  压摆率对于大信号处理是一个很重要的指标，对于要求比较高的运放一般SR＞10V/μs。通过图1我们大家可以认为其实压摆率就是一个爬升过程，压摆率越大爬升越快，越小爬升越慢，意味着在信号到来时，不能准确的跟上，当跟上时，信号已经消失流走了，使得只能跟上一半或者更低，这样就容易失真。或者说压摆率就是个斜率，斜率越陡压摆率越大。